Hyperbolic Functions

Hyperbolic cosine is ${\color{red}{{{y}={\cosh{{\left({x}\right)}}}=\frac{{{{e}}^{{x}}+{{e}}^{{-{x}}}}}{{2}}}}}$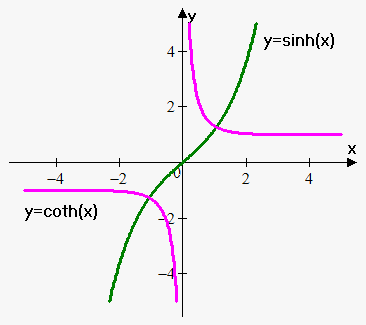 . hyperbolic sine and hyperbolic cotangent

Hyperbolic sine is ${\color{blue}{{{y}={\sinh{{\left({x}\right)}}}=\frac{{{{e}}^{{x}}-{{e}}^{{-{x}}}}}{{2}}}}}$ .

Hyperbolic tangent is ${\color{green}{{{y}={\tanh{{\left({x}\right)}}}=\frac{{{\sinh{{\left({x}\right)}}}}}{{{\cosh{{\left({x}\right)}}}}}=\frac{{{{e}}^{{x}}-{{e}}^{{-{x}}}}}{{{{e}}^{{x}}+{{e}}^{{-{x}}}}}}}}$ .

Hyperbolic cotangent is $y=\coth\left(x\right)=\frac{\cosh\left(x\right)}{\sinh\left(x\right)}=\frac{e^{x}+e^{-x}}{e^{x}-e^{-x}}$ .

Hyperbolic secant is ${y}=\operatorname{sech}{\left({x}\right)}=\frac{{1}}{{{\cosh{{\left({x}\right)}}}}}=\frac{{2}}{{{{e}}^{{x}}+{{e}}^{{-{x}}}}}$ .

Hyperbolic cosecant is ${y}={\operatorname{csch}{{\left({x}\right)}}}=\frac{{1}}{{{\sinh{{\left({x}\right)}}}}}=\frac{{2}}{{{{e}}^{{x}}-{{e}}^{{-{x}}}}}$ .

There is some similarity between hyperbolic functions and trigonometric.

hyperbolic cosine and hyperbolic tangent Domain of hyperbolic functions is ${\left(-\infty,\infty\right)}$ , except for function ${y}={\coth{{\left({x}\right)}}}$ which is undefined when ${x}={0}$ .

Formulas that hold for any ${x}$ and ${y}$ :

${\cosh{{\left({x}\pm{y}\right)}}}={\cosh{{\left({x}\right)}}}{\cosh{{\left({y}\right)}}}\pm{\sinh{{\left({x}\right)}}}{\sinh{{\left({y}\right)}}}$ .
${\sinh{{\left({x}\pm{y}\right)}}}={\sinh{{\left({x}\right)}}}{\cosh{{\left({y}\right)}}}\pm{\cosh{{\left({x}\right)}}}{\sinh{{\left({y}\right)}}}$ .
${{\cosh}}^{{2}}{\left({x}\right)}-{{\sinh}}^{{2}}{\left({x}\right)}={1}$ .
${\cosh{{\left({2}{x}\right)}}}={{\cosh}}^{{2}}{\left({x}\right)}+{{\sinh}}^{{2}}{\left({x}\right)}$ .
${\sinh{{\left({2}{x}\right)}}}={2}{\sinh{{\left({x}\right)}}}{\cosh{{\left({x}\right)}}}$ .

This formulas can be easily proved using definitions of hyperbolic functions.