1. Home
  2. Math Notes
  3. Calculus I
  4. Common Functions

Rational Function

Function of the form $$${f{{\left({x}\right)}}}=\frac{{{Q}{\left({x}\right)}}}{{{P}{\left({x}\right)}}}=\frac{{{a}_{{0}}{{x}}^{{n}}+{a}_{{1}}{{x}}^{{{n}-{1}}}+\ldots+{a}_{{{n}-{1}}}{x}+{a}_{{n}}}}{{{b}_{{0}}{{x}}^{{m}}+{b}_{{1}}{{x}}^{{{m}-{1}}}+\ldots+{b}_{{{m}-{1}}}{x}+{b}_{{m}}}}$$$, where $$${Q}{\left({x}\right)}$$$ and $$${P}{\left({x}\right)}$$$ are polynomials is called rational function.

Domain of this function consists of all $$${x}$$$ such that $$${Q}{\left({x}\right)}\ne{0}$$$.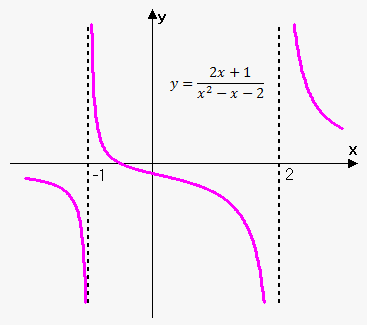rational function

Simple example of the rational function is $$${f{{\left({x}\right)}}}=\frac{{{2}{x}+{1}}}{{{{x}}^{{2}}-{x}-{2}}}=\frac{{{2}{x}+{1}}}{{{\left({x}-{2}\right)}{\left({x}+{1}\right)}}}$$$. Its domain is all $$${x}$$$ except $$${x}={2}$$$ and $$${x}=-{1}$$$.

This function is shown on the figure.