Trigonometric Functions

Consider unit circle centered at origin and point ${P}_{{0}}{\left({1},{0}\right)}$. If we begin to rotate point ${P}_{{0}}$ around origin on angle ${t}$ then we will obtain point ${P}_{{t}}$.

x-coordinate of this point is called cosine of number ${t}$ and denoted by ${\cos{{\left({t}\right)}}}$, y-coordinate of this point is called sine of number ${t}$ and denoted by ${\sin{{\left({t}\right)}}}$.

When we talk about trigonometric functions we can use both radian and degree measure of angle ${t}$, but in calculus we almost always use radian measure (unless other stated).

To convert radian measure to degree and vice versa following formulas are used:

${1}\ {r}{a}{d}=\frac{{{{180}}^{{0}}}}{\pi}\approx{{57}}^{{0}}$ and ${{1}}^{{0}}=\frac{\pi}{{{{180}}^{{0}}}}\ {r}{a}{d}\approx{0.017}\ {r}{a}{d}$.

So, $\pi$ is ${{180}}^{{0}}$, ${2}\pi$ is ${{360}}^{{0}}$, $\frac{\pi}{{2}}$ is ${{90}}^{{0}}$ etc.

Domain of cosine and sine is ${\left(-\infty,\infty\right)}$, their range is ${\left[-{1},{1}\right]}$.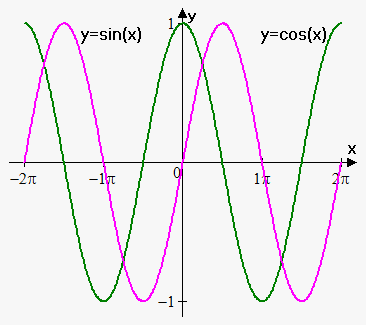

These functions are periodic with main period ${2}\pi$, i.e. ${\sin{{\left({x}+{2}\pi\right)}}}={\sin{{\left({x}\right)}}}$ and ${\cos{{\left({x}+{2}\pi\right)}}}={\cos{{\left({x}\right)}}}$ for all ${x}$.

Domain of tangent function is all ${x}$ except those ${x}$ where ${\cos{{\left({x}\right)}}}={0}$.

Range of tangent function is ${\left(-\infty,\infty\right)}$.

Tangent is periodic function with period $\pi$: ${\tan{{\left({x}+\pi\right)}}}={\tan{{\left({x}\right)}}}$ for all ${x}$.

Domain of cotangent function is all ${x}$ except those ${x}$ where ${\sin{{\left({x}\right)}}}={0}$.

Range of cotangent function is ${\left(-\infty,\infty\right)}$. Cotangent is periodic function with period $\pi$: ${\cot{{\left({x}+\pi\right)}}}={\cot{{\left({x}\right)}}}$ for all ${x}$.

Trigonometric functions, because of periodicity, are widely used for modeling repetitive events: motion of pendulum, vibrating string, sound waves etc.