Area Problem
Suppose that we are given continuous function $$$y={f{{\left({x}\right)}}}$$$ on $$${\left[{a},{b}\right]}$$$ such that $$${f{{\left({x}\right)}}}\ge{0}$$$ for all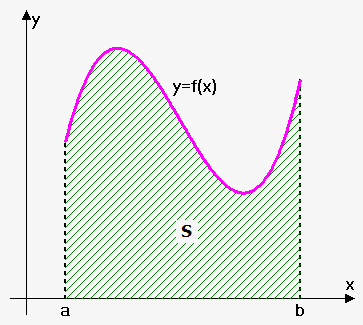 
$$${x}\in{\left[{a},{b}\right]}$$$.
We want to find area $$${S}$$$ that lies under curve $$${f{{\left({x}\right)}}}$$$ and bounded by lines $$${x}={a}$$$, $$${x}={b}$$$ and x-axis.
Before doing this imagine right bound $$${b}$$$ is not fixed, we can move it. Then for different values of right bound we will obtain different values of area, so we can consider area as function $$${P}{\left({x}\right)}$$$ of right bound. In particular, $$${P}{\left({a}\right)}={0}$$$ (because area from $$${a}$$$ to $$${a}$$$ is 0) and $$${P}{\left({b}\right)}={S}$$$.
To get a better understanding what is $$${P}{\left({x}\right)}$$$ consider next example.
Example 1. Consider function $$${y}={x}-{1}$$$. If $$${P}{\left({x}\right)}$$$ represents area of figure under $$${y}={x}$$$, above x-axis on interval $$${\left[{1},{x}\right]}$$$ find $$${P}{\left({1}\right)}$$$, $$${P}{\left({2}\right)}$$$, $$${P}{\left({3}\right)}$$$ and $$${P}{\left({4}\right)}$$$.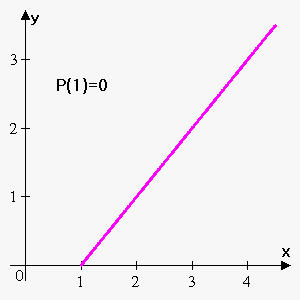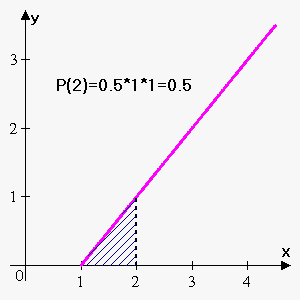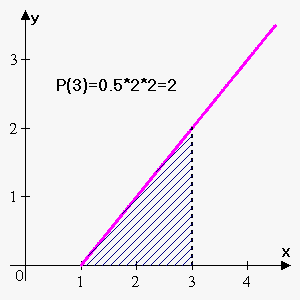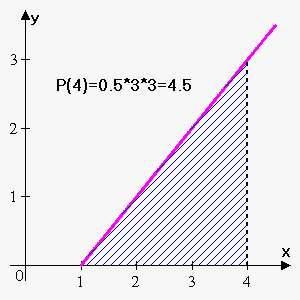
$$${P}{\left({1}\right)}$$$ is area on interval $$${\left[{1},{1}\right]}$$$, so it is 0 (because length of interval is 0).
$$${P}{\left({2}\right)}$$$ is area on interval $$${\left[{1},{2}\right]}$$$. It is area of right-angled triangle with legs 1 and 1. So, $$${P}{\left({2}\right)}=\frac{{1}}{{2}}\cdot{1}\cdot{1}=\frac{{1}}{{2}}$$$.
$$${P}{\left({3}\right)}$$$ is area on interval $$${\left[{1},{3}\right]}$$$. It is area of right-angled triangle with legs 2 and 2. So, $$${P}{\left({3}\right)}=\frac{{1}}{{2}}\cdot{2}\cdot{2}={2}$$$.
$$${P}{\left({4}\right)}$$$ is area on interval $$${\left[{1},{4}\right]}$$$. It is area of right-angled triangle with legs 3 and 3. So, $$${P}{\left({4}\right)}=\frac{{1}}{{2}}\cdot{3}\cdot{3}=\frac{{9}}{{2}}$$$.
As can be seen $$${P}{\left({x}\right)}$$$ is indeed function: for any particular value of $$${x}$$$ there is corresponding $$${P}{\left({x}\right)}$$$.
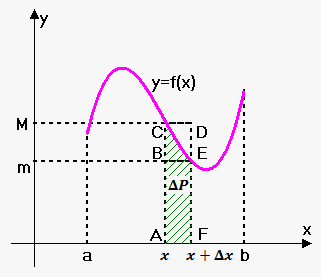
Now, suppose we want to find derivative of $$${P}{\left({x}\right)}$$$. For this increase $$${x}$$$ by $$$\Delta{x}$$$. Corresponding increase in area is $$$\Delta{P}={P}{\left({x}+\Delta{x}\right)}-{P}{\left({x}\right)}$$$ (figure ACEF).
If we denote maximum and minimum value of $$${f{{\left({x}\right)}}}$$$ on interval $$${\left[{x},{x}+\Delta{x}\right]}$$$ by $$${M}$$$ and $$${m}$$$ respectively, then area of figure ACEF is less than area of rectangle ACDF and greater than area of rectangle ABEF.
Since area of rectangle ACDF is $$${M}\Delta{x}$$$ (height multiplied by base)and area of rectangle ABEF is $$${m}\Delta{x}$$$ then
$$${m}\Delta{x}<\Delta{P}<{M}\Delta{x}$$$ or $$${m}<\frac{{\Delta{P}}}{{\Delta{x}}}<{M}$$$.
Now let $$$\Delta{x}\to{0}$$$. Since $$${f{}}$$$ is continuous then both $$${m}$$$ and $$${M}$$$ approach $$${f{{\left({x}\right)}}}$$$.
Thus, by Squeeze Theorem $$$\lim_{{\Delta{x}\to{0}}}\frac{{\Delta{P}}}{{\Delta{x}}}={f{{\left({x}\right)}}}$$$.
But we recognize in $$$\lim_{{\Delta{x}\to{0}}}\frac{{\Delta{P}}}{{\Delta{x}}}$$$ derivative of $$${P}{\left({x}\right)}$$$, so $$${P}'{\left({x}\right)}={f{{\left({x}\right)}}}$$$.
In other words $$${P}{\left({x}\right)}=\int{f{{\left({x}\right)}}}{d}{x}={F}{\left({x}\right)}+{C}$$$.
Since $$${P}{\left({a}\right)}={0}$$$ then $$${0}={P}{\left({a}\right)}={F}{\left({a}\right)}+{C}$$$ or $$${C}=-{F}{\left({a}\right)}$$$.
Therefore, $$${P}{\left({x}\right)}={F}{\left({x}\right)}-{F}{\left({a}\right)}$$$.
Newton-Leibniz Formula. Area of figure $$${P}{\left({x}\right)}$$$ that lies under curve $$${y}={f{{\left({x}\right)}}}$$$, above x-axis on interval $$${\left[{a},{x}\right]}$$$ is $$${P}{\left({x}\right)}={F}{\left({x}\right)}-{F}{\left({a}\right)}$$$.
Returning to our initial problem we have that $$${S}={F}{\left({b}\right)}-{F}{\left({a}\right)}$$$.
Area of figure that lies under curve $$${y}={f{{\left({x}\right)}}}$$$, above x-axis and between lines $$${x}={a}$$$ and $$${x}={b}$$$ is $$${S}={F}{\left({b}\right)}-{F}{\left({a}\right)}$$$ where $$${F}$$$ is antiderivative of $$${f{}}$$$.
Example 2. Find area under $$${y}={{x}}^{{2}}$$$, above x-axis on interval $$${\left[{0},{2}\right]}$$$.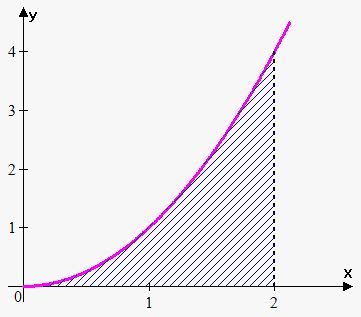
We have that $$${F}{\left({x}\right)}=\int{{x}}^{{2}}{d}{x}=\frac{{1}}{{3}}{{x}}^{{3}}$$$ (note that we need particular derivative here).
Now, according to Newton-Leibniz Formula required area is $$${S}={F}{\left({2}\right)}-{F}{\left({0}\right)}=\frac{{1}}{{3}}\cdot{{2}}^{{3}}-\frac{{1}}{{3}}\cdot{{0}}^{{3}}=\frac{{8}}{{3}}$$$.
All from above can be easily extended on case when function can take negative values. For this we only need to consider areas under x-axis negative.
Indeed, if we want to find area enclose by parabola $$${y}=-{{x}}^{{2}}$$$, x-axis on interval $$${\left[{0},{2}\right]}$$$ then according to Newton-Leibniz Formula we have that $$${S}={F}{\left({2}\right)}-{F}{\left({0}\right)}$$$ where $$${F}{\left({x}\right)}=\int-{{x}}^{{2}}{d}{x}=-\frac{{1}}{{3}}{{x}}^{{3}}$$$. So, $$${S}=-\frac{{8}}{{3}}$$$. Since $$$-{{x}}^{{2}}$$$ is reflection of $$${{x}}^{{2}}$$$ about x-axis then this area lies below x-axis, and, therefore, negative.